Database(6) -- Relational Algebra

LeetCode Day 35: P219. Contains Suplicate II (Easy)

题目：

一个数组， 判定是否存在两的相同的数字，它们的索引差小于等于k。

我的思路:

用HashMap记录所有数字的索引值，只要找到重复的数字，就算一个索引的差值，并保留最小的差值。 最后看这个差值是否小于k。

我的代码：

public class E_219_ContainsDuplicateII {
    public static boolean containsNearbyDuplicate(int[] nums, int k) {
        int distance = Integer.MAX_VALUE;
        HashMap<Integer, Integer> hashMap = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            if (!hashMap.containsKey(nums[i])) {
                hashMap.put(nums[i], i);
            } else {
                int temp = i - hashMap.get(nums[i]);
                if(temp < distance) {
                    distance = temp;
                }
                hashMap.put(nums[i], i);
            }
        }
        return distance <= k;
    }

    public static void main(String[] args) {
        int[] test1 = {1,2,3,1,2,3};
        System.out.println(containsNearbyDuplicate(test1, 2));
        int[] test2 = {1,0,1,1};
        System.out.println(containsNearbyDuplicate(test2, 1));
    }
}

超过80%

最优解：

class Solution {
    public boolean containsNearbyDuplicate(int[] nums, int k) {
        if(k > 3000)
            return false;
        if(nums.length < 2 || k < 1)
            return false;
        Set<Integer> set = new HashSet<Integer>();

        for(int i = 0 ; i < nums.length; i++){
            if(set.contains(nums[i]))
                return true;
            set.add(nums[i]);
            if(set.size() > k)
                set.remove(nums[i-k]);
        }
        return false;
    }
}

只用一个HashSet，用k作为set的最大容量。只要在这个范围内出现了重复，就直接返回true。每次删除前面距离太远的那些数。这就意味着不需要遍历完整个数组，很可能就已经找到答案了。

Database

Relational Algebra

Relational Algebra: construct new relations from given relations. SQL incorporates relational algebra at its center. SQL query is translated into relational algebra.

SQL can do less than C or Java, so the compiler can produce highly optimized code.

Relational algebra:

1. Relations are Variables
2. finite relations are constants

Operations:

1. set operations – union, intersection, difference
2. Removing – “selection eliminates some rows, and “projection” eliminates some columns.
3. Combine the tuples of two relations – Cartesian product, “join” operations.
4. Renaming – names of the attributes and/or the name of the relation itself.

Set operations on Relations

1. R and S must have schemas with identical sets of attributes, and the types must be the same.
2. The columns of R and S must be ordered.

Projection (Column)

The projection operator is used to produce from a relation R a new relation that has only some of R’s columns. π A1,A2,…,An(R) is a relation that has only the columns for attributes A1, A2,…,An of R. For example:

π title,year,length(Movies)

Selection (Row)

The selection operation produces a new relation with a subset of R’s tuples that satisfy some conditin C. σC(R). For example:

• σlength>=100(Movies)
• σlength>=100 AND studioName=’Fox’(Movies)

Cartesian Product

The result of pairing a tuple from R with a tuple from S is a longer tuple, with one component for each of the components of the constituent tuples.

Natural Joins

R ⨝ S only pair tuples that are agree in common attributes.

• Joined tuple: with one component for each of the attributes in the union of the schemas of R and S.

Theta-Joins

Pair tuples from two relations on some other basis.

R ⨝_C S

1. Take the product of R and S.
2. Select from the product only those tuples that satisfy the condition C.

Combining Operations

Expression Tree:

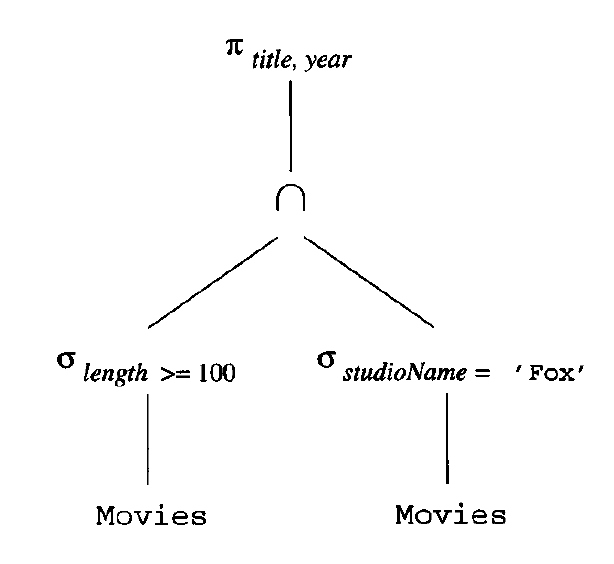
Linear Notation:

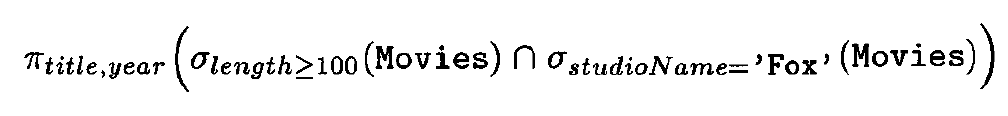
Naming and Renaming

ρS(A1,A2,…,An)(R)

Relationships Among Operations

R ∩ S = R - (R - S)

R ⨝_C S = σ_C(R * S)